冬至は一年で一番日の出の遅い日か？・・・均時差の話
●冬至は一年で一番日の出の遅い日か？
（夏至は一年で一番日の出が早い日か？　でもいいですけど）

または、
●正午は太陽は南中するか？

冬至の時期になれば、「冬至は一年で一番昼が短くなる日」と言う解説が流れ、半年の間を置いた夏至の時期には「夏至は一年で一番昼が長い日」と似たような話しがニュースや天気予報の時間にながされます。
この説明はそのとおり。
普通の方は大体この説明でご満足いただけるようですが、たまに「と言うことは、冬至の日は日の出が一番遅い日（夏至なら日の出が早い日）か」

と調べてみようとする念の入った方がいます。そして、念を入れた甲斐あって「違うぞー！」と言う結果に辿り着く。
そして、「理由が解らないと気になって眠れない」という方からこよみのページへと質問が寄せられる結果になる。
（お陰様で賑わってます？）

ではこれからゆっくりその話しをして行きましょう。

時刻はどうして決まる（太陽時今昔物語）

真太陽時（視太陽時）の発見と、その時代
現在日常で使われる時刻は太陽を基準とした「太陽時」と言うものです。
簡単に言ってしまうと、「太陽が真南に来た時から、次に真南に来るまでの時間を測って１日（１太陽日）とする。」と言うもの。
１日の長さが決まればそれを２４等分すると１時間が決まり、１時間を６０等分すると１分が決まり、１分を６０等分すると１秒が決まるというわけです。

太陽がこのように１日に空（天文学では「天球」と言います）を一回りする主な理由は地球の自転運動ですが、地球が自転で１回転する間に、地球は太陽の周りの軌道を約１度ほど移動してしまいます（地球の公転運動）ので、この１度を加えた「１回転＋１度」あまり自転する時間が太陽を基準とした１日となります。

このようにして１日の長さを太陽の動きで決めるようになったのは、おそらく数千年以上も前。こうして決めた時刻は実際に視た太陽（視太陽と言う）を基準にしたと言うことから、視太陽時または、真太陽時と呼ばれます。
真太陽時による時刻系の発明時期は、天文学の黎明期であったと考えられます。
それから数千年、この視太陽時は日常生活を送る上で重要な時刻系として使われてきました。

---

平均太陽時の発明とその時代
のどかな時代が数千年続いた後、世の中はせかせかとした「工業化時代」を迎えてしまいました。

この時代になると正確な機械時計が作られるようになりました。すると今まで使ってきた真太陽時の大きな欠点が目に付くようになりました。
その欠点とは・・・季節によって１日の長さが変化する・・・と言うことです。
時間の基準となる１日の長さが季節によって違うとなれば、時分秒も季節毎に違うことになり、困った問題が起きてしまいます。

そこで、季節毎にまちまちの１日の長さを平均した「平均太陽日」を時間の尺度に使用言うことになり、これに基づいた平均太陽時がそれまでの真太陽時に取って代わりました。

---

平均太陽時と「平均太陽」
平均太陽時は、天球上の赤道（天の赤道）を一定速度で移動する「平均太陽」という仮想の天体に基づいた時刻系と考えることが出来ます（あくまでも仮想の天体ですので見えませんけどね）。

均時差とは
均時差とは「視（真）太陽と平均太陽の時角差」です。
ちょっと解りにくいので、次のように考えてみて下さい。
日本標準時の基準となる東経１３５度の場所では、「正午」に平均太陽は真南にあるはずです（「南中」）。しかしこのとき本物のの太陽（視太陽）は必ずしも南中しているとは限りません。
本当の太陽は何分か前か後かに南中するわけですが、この時間の差がすなわち均時差と考えることが出来ます。

（図１）平均太陽と視太陽

左の図では
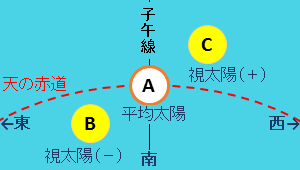　Ａ　　：平均太陽
　Ｂ，Ｃ：視太陽
をそれぞれ表しています（Ｂ，Ｃの違いは、季節の違いと思って下さい）。

冬至が日の出が一番遅い日でないわけ
ここでようやく最初の質問に戻ります。

---

注意
厳密な話しを始めるといろいろ考えないといけない要素が増えて収拾がつかなくなりますので、いろいろ省略しています（時間に関しては１分程度の精度まで）。
厳密に・・・と言う方は、自分でもっと勉強してね。

---

日の出から太陽（ここでは本物の太陽・・・視太陽）が南中するまでの時間と、南中してから陽が沈む間での時間は同じと考えることが出来ます。ならば、均時差が「０」だとすると
　（均時差が無い場合の式）
　日の出時刻 = 12時-(昼の時間 / 2)
　日の入時刻 = 12時+(昼の時間 / 2)

となります。とすれば、昼の時間が短い程日の出は遅く、日の入は早い時間となります。つまり、冬至の日が日の出が一番遅い日（夏至の日は日の出が一番早い日）となるのです。

しかしここに均時差が入りますと式は次の様に変わります。
　（均時差を考慮した場合の式）
　日の出時刻 = 12時-(昼の時間 / 2) - 均時差
　日の入時刻 = 12時+(昼の時間 / 2) - 均時差

北緯35度付近で実際の計算をしてみましょう。
冬至の日と日の出の一番遅くなる日（1/7頃）での日の出の例です。
（参考までに、日の入の時刻も）

昼の時間   均時差   答え 冬至の日の出   12時 - ( 9時間48分 / 2) - 2分 = 7時04分頃 1/7頃の日の出   12時 - ( 9時間56分 / 2) - (-6)分 = 7時08分頃 冬至の日の入   12時 + ( 9時間48分 / 2) - 2分 = 16時52分頃 1/7頃の日の入   12時 + ( 9時間56分 / 2) - (-6)分 = 17時04分頃

どうですか？
昼の長さは８分ほど冬至の日頃の方が短いですが、均時差を考慮すると1/7の方が日の出の時刻が遅くなることがわかりますね。
次のグラフは一年を通して、均時差によって日の出日の入りの時刻がどのように変化するかを示したものです（年毎の変化はほとんどありません）。

（図２）均時差による日出没時刻のズレ
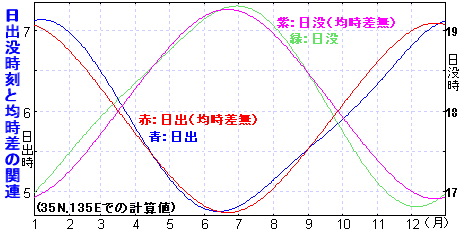青線 日の出時刻 赤線 日の出時刻　（均時差が無い時） 緑線 日の入時刻 紫線 日の入時刻　（均時差が無い時）

均時差が生ずる理由

均時差が発生する理由は２つあります。
１．地球の軌道が円でないために起こる、太陽の黄経変化の不均一。
２．黄道面と赤道面が一致していない（傾いている）。

順を追って説明してみましょう。

●地球の軌道が円でないために起こる、太陽の黄経変化の不均一。 地球は１太陽日の間に 360度 + α だけ自転しています。
この「α」は地球が太陽の周りを公転しているため、地球が360度自転している間に、約 360/365.25度≒約1度 だけ太陽の周りを回っていて、太陽の見かけの位置が変化しますのでその分余分に自転する必要があるわけです。
ついでですがこのとき、太陽が移動して行く道筋は「黄道」と呼ばれています。

もし、地球が円軌道を描いて太陽の周りを回っていれば、この「α」は常に一定です。
ところが、地球の公転軌道は円軌道ではなく、わずかに扁平な楕円軌道です。そうすると太陽に近いときは平均より早く、遠いときは平均より遅く移動します（ケプラーの第二法則・・・って覚えてましたか？）ので、太陽の見かけの動きにも遅速があるわけです。
季節によって、太陽の黄道上の移動速度がどのように変わるかを示した図を次に示します（一日毎の移動量です）。

（図３）地球の軌道が楕円であるために起こる黄経移動量の変化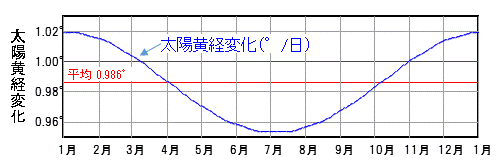

●黄道面と赤道面が一致していない（傾いている）。 太陽の通り道を黄道と言うのに対して、地球の自転軸に直交する面を赤道と呼びます。地球上の赤道を天球まで投影したものと考えると解りやすいかも知れません。

さて、この黄道と赤道が一致していれば問題は無かったのですが、実際にはこの２つは約23.4度の角度で交差しているのです（このために、四季の気候変化が起こるわけですが）。

このため仮に太陽が黄道上を一定速度で移動していたとしても、太陽が赤道との交点付近いる場合と、赤道から一番離れた点にあるときでは赤道座標における経度変化量は違ってきます。この見かけ上の変化は、
　春分・秋分点付近で最小
　　≒ cos(23.4度) ≒ 0.9178(倍)
　冬至・夏至点付近で最大
　　≒ sec(23.4度) ≒ 1.0896(倍)
に拡大されます。
ここで登場した23.4度は、黄道と赤道の傾斜角です。

---

補足説明
赤道と黄道の交点付近（春分・秋分点付近）では、赤経１度と黄経１度の天球上での長さは
　　1.0 : 1.0
と考えられますが、この付近では赤道と黄道の傾斜角23.4度がそのまま影響します。そのため、黄経１度の変化は、
　　１度×cos(23.4度)
の赤経変化となります。

これに対して、冬至・夏至付近では、赤経１度と黄経１度の天球上での長さは
　　1.0 × cos(23.4) : 1.0
となりますが、赤道と黄道の傾斜による効果は無視できるほど小さくなるため、黄経１度の変化は
　　１度／cos(23.4度) = １度×sec(23.4度)
の赤経変化となります。

---

季節毎の拡大率をグラフ化して次ぎに示します。

（図４）赤道と黄道の傾斜による赤経変化の拡大率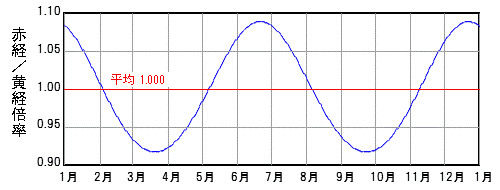

●さて、二つの効果が複合すると。 仮想の平均太陽の赤道上の移動速度（赤経方向のみの変化です）は軌道が楕円のために起こる運動と、黄道・赤道面の傾斜による変化量の拡大率双方の平均値を持つ天体と考えることが出来ます。
平均値は前者が 0.986,後者が 1.000ですから平均の赤経移動量は

　0.986 × 1.000 = 0.986 (度／日)

と言うことになります。このペースで移動すると360度変化するには
　360度 / 0.986度 = (約)365日
つまり、１年かけて１周りする事になるのです。
平均太陽日は、この仮想天体である平均太陽が南中してから再び南中する間での長さと同じわけですから、その間に地球は
　360 + 0.986 = 360.986 (度)
自転します。これだけ自転するのに要する時間が日常使う24時間になります。

均時差とは、要はこの平均との各部分での差が生み出すもの。例として冬至に近い１月初めと春分に近い４月初めの値をグラフから読みとって考えてみましょう。

（計算例）１月初めと４月初めに発生する日毎のズレの量

時期	平均値	−	楕円効果	×	赤経拡大	＝	差（度）	（差の時間）
１月	0.986	−	1.020	×	1.083	＝	-0.119（度）	-28.5秒
４月	0.986	−	0.987	×	0.920	＝	+0.078（度）	+18.7秒

最後の差の時間は、角度の差 / (360 + 0.986) × 86400秒 としたものです。一日毎にこれだけの差が生じるわけです。
この値は小さい物のようですが、この差が数十日も積み重なるとかなりの量になり、目に見える均時差となるわけです（ようやく結論・・・）。

さて、説明した２つの効果が複合されると、実際の均時差となります。下の図は
　視（真）太陽の時角 - 平均太陽の時角
を表しています。こうして視ると均時差は以外に大きく、最大で15分を越えることもあるのです。

（図５）均時差の季節変化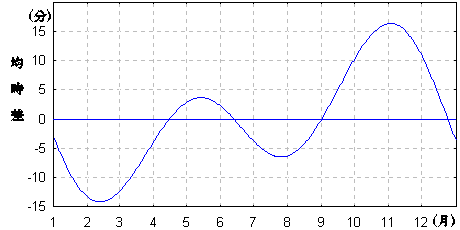

余　談

今回は、もっとさらっと書くつもりだったし、簡単に書くはずだったけど、結果はご覧の通り。
思いの外疲れました。